Kompresja kodem arytmetycznym (MATLAB) obrazu śmieszka - skala szarości

Kodowanie arytmetyczne to metoda kodowania źródłowego dyskretnych źródeł sygnałów, stosowana jako jeden z systemów w bezstratnej kompresji danych. Została wynaleziona przez Petera Eliasa około 1960 roku. Ideą tego kodu jest przedstawienie ciągu wiadomości jako podprzedziału przedziału jednostkowego [0,1) wyznaczonego rekursywnie na podstawie prawdopodobieństw wystąpienia tychże wiadomości generowanych przez źródło. Ciąg kodowy reprezentujący kodowane wiadomości jest binarnym zapisem wartości z wyznaczonego w ten sposób przedziału

Można udowodnić, że przy wyborze odpowiednio długiego ciągu wiadomości do zakodowania, średnia liczba symboli na wiadomość jest mniejsza od H(X) + 2, gdzie H(X) jest entropią źródła, lecz większa bądź co najwyżej równa samej entropii.

Dany jest zbiór symboli

oraz stowarzyszony z nim zbiór prawdopodobieństw

. Jeden z symboli jest wyróżniony - jego wystąpienie oznacza koniec komunikatu, zapobiegając wystąpieniu niejednoznaczności; ewentualnie zamiast wprowadzenia dodatkowego symbolu można przesyłać długość kodowanego ciągu.
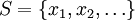
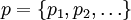
Na początku dany jest przedział P = [0,1), który dzielony jest na podprzedziały o szerokościach równych kolejnym prawdopodobieństwom pi, czyli otrzymywany jest ciąg podprzedziałów


, .... Kolejnym podprzedziałom (ozn. Ri) odpowiadają symbole ze zbioru S.

Algorytm kodowania:
* Dla kolejnych symboli symbol c.
o Określ, który podprzedział bieżącego przedziału P odpowiada literze c - wynikiem jest Ri.
o Weź nowy przedział P: = Ri - następuje zawężenie przedziału
o Podziel ten przedział P na podprzedziały w sposób analogiczny jak to miało miejsce na samym początku (chodzi o zachowanie proporcji szerokości podprzedziałów).
* Zwróć liczbę jednoznacznie wskazującą przedział P (najczęściej dolne ograniczenie, albo średnia dolnego i górnego ograniczenia).

Przykład 1
Na rysunku pokazano, jak zmienia się aktualny przedział P w trzech pierwszych krokach kodowania. Kodowane są cztery symbole o prawdopodobieństwach p = {0.6,0.2,0.1,0.1} w kolejności: pierwszy, trzeci, czwarty.

źródło materiału: